)
where I is the intensity in watts/m
. The unit is decibel, denoted "dB". For the hearing
threshold, I/
= 1 and SL = 0 dB. For the feeling threshold, I/ = 10
= 120 dB.Comparison of Sound Intensity Level (SL)
and
Sound Pressure Level (SPL)
SL = 10 x log (I/)
where I is the intensity in watts/m. The unit is decibel, denoted "dB". For the hearing
threshold, I/
= 1 and SL = 0 dB. For the feeling threshold, I/ = 10 = 120 dB.
Note that when a quantity is expressed in decibels a relative measure is
given. That is, it is given with respect to some reference value ( in the case of SL). Whenever the
intensity (I) is multiplied by a factor of 10, one just adds ten decibels
to the value of SL. Whenever the intensity is multiplied by a factor of 100,
one just adds 20 decibels to the value of SL.
Now, there is a relation between the intensity of a sine sound wave (I) and the
value of the average pressure variation Dp. (Dp= pressure variation amplitude
divided by 2.) 
where V is the velocity of sound in air and 
is the air density. For normal conditions
of air and temperature,
I = 0.00234 x Dp.
Dp is in Newton/m
.
Now the threshold of hearing is 10
watt/m.
According to this expression for I above, this represents an average pressure variation
of only 2.0 x 10
Newton/m.
This relation also shows that I is proportional to the square of Dp, thus
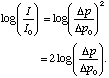
Thus the quantity Sound Pressure Level (SPL):
SPL = 20 log 
.
For a travelling wave, the numerical values of SL and SPL are identical and SPL and SL are one and the same thing.
Now, for standing waves, there is no energy flow at all and the intensity I cannot be defined, hence SL loses its meaning. Yet the concept of average pressure variation Dp at a given point in space (at the entrance to the auditory canal for example) remains meaningful. That is why SPL is more frequently used than SL.