 |
There is something satisfying about musical sounds that blend and harmonize. However,
some combinations of sounds are unpleasant.
This section fo the course beirfly examines some of the characteristics of our ear/brain
hearing system in order to explain why some basic sounds sound pleasant, and some
sound raucous and unpleasant.
Music involves such highly complex sounds that trying to analyze just what is affecting
what on is very difficult.
So, in order to simplify the issues, we use pure tones to probe into the question
of why some tonal combinations sound good and some do not. We shall base this exercise
on a tone of 500 Hertz at a comfortable listening level: AUDIO
Now listen to a second tone, an identical 500 Hertz of the same amplitude: (make
sure your playback sysem is loud enough to hear the differences) AUDIO
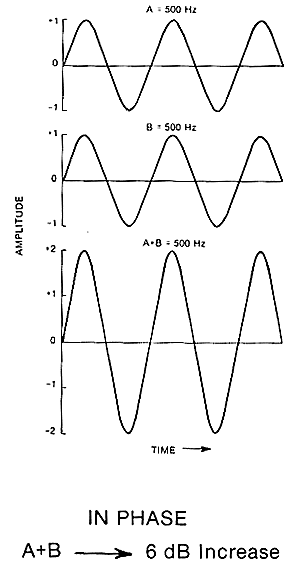
Notice that there is an increase in loudness. Thi is because the two sine waves
have a time relationship described as being "in phase." (see diagram).
Because the two tones are in phase, they add constructively (2 +'s make a +) and
the resulting combination has twice the amplitude of either single tone hear alone.
Adding two waves of the same frequency, amplitude and phase produces a 6 decibel
increase in signal level. Refer back to the loudness
section of the course if you're unsure why. |
 |
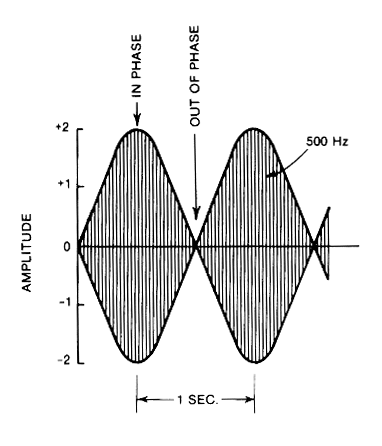
Now, listen to what happens if the same two 500 Hertz sine waves are combined "out
of phase" or in "phase opposition", that is, when one waveform goes
positive, the other goes negative and vice versa.
First, one signal alone: AUDIO
And now the second tone will be added momentarily and then taken away: AUDIO
That dead spot in the middle was caused by adding the second, equal 500 Hertz
tone out of phase. When the two signals are in "phase opposition", one
cancels the other and the resultant output is zero. |
|
|
The previous examples used signals of the same frequency. When two tones of differing
frequency are combined, some very interesting things happen that have a direct bearing
on our sense of musical sounds. A tone of 500 Hertz added to a tone of 501 Hertz
sounds like this: AUDIO
The two tones, only 1 Hz apart, alternately combine in phase and phase opposition
to produce a 1 Hz beat.
By holding the 500 Hertz tone constant and changing the frequency of the second tone,
the beat frequency can be varied in a regular way: AUDIO
The frequency of the beating is determined by the difference between the frequencies
of the two tones which are heard together. Thus, if a tone of either 490 Hertz or
500 Hertz is combined with the 500 Hertz tone, a beat of 10 Hertz is produced.
As the difference between the two tones is increased so that the beat frequency increases
to about 20 Hertz, the ear becomes unable to discern the individual beats: AUDIO
Beyond 20 Hertz, a harsh, rattling sound is heard: AUDIO
Note the roughness! It is the basis of what we consider to be unpleasant musical
effects, as we shall see later. |
 |
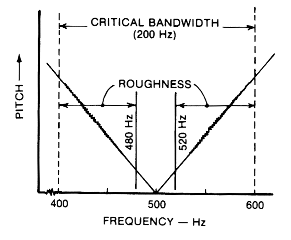 |
The critical band seems to be involved in what we hear
wehn two tones which are sounded together. If the two tones are a critical bandwidth
apart, they are heard, not as beats or roughness, but as two separate tones.
In the following example, notice the transition from beats, through roughness, to
a more pleasant or settled sound as the two combined tones are increasingly separated
in frequency: AUDIO
To avoid the region of roughness, and for the ear to separate the two tones,
they must be at least a critical bandwidth apart.
When tones are sounded simultaneously, the result may be considered as either pleasant
or unpleasant. Another way of describing these sensations is with the terms consonant
or dissonant. In a psychoacoustical context, the term "consonance"
means tonal, or sensory consonance. This is distinguished from the way musician's
use of the word, which is dependent on Helmholtz frequency ratios, music theory and
is in fact ultimately culturally defined. In this contecxt we are referring to a
human perception. Of course, in an ultimate sense, the two definitions are related.
NB. The audibility of these roughness effects does NOT depend upon musical training. |
 |
Now consider the same beating effect between two tones in terms of their separation
in fractions of a critical bandwidth. As we have seen, at 500 Hertz the critical
band is somewhere around 100 Hertz wide. Let us define 100 Hertz as "unity"
and consider fractions of that band.
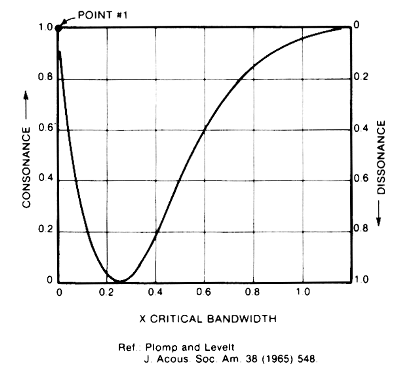
When two tones have zero separation, they sound as a single tone which has maximum
consonance and minimum dissonance. AUDIO
That is point number #1 on our curve.
And now, here are the two tones separated by about 1/4 of a critical bandwidth:
AUDIO
This is the least consonant, or the most dissonant, sound.
When the two tones are separated by about one-half a critical bandwidth, the roughness
has partially receded to give us about 40 percent of full consonance: AUDIO
At a separation of about 3/4s of a critical bandwidth, a further improvement
in consonance, to about 80 percent, is noted: AUDIO
When two tones separated by a full critical bandwidth are combined, 100 percent
consonance results: AUDIO AUDIO(sgi)
This puts the effects of combining two tones into perspective:
• If their frequencies are separated by a critical bandwidth, or more, the effect
is consonant.
• If their frequencies are separated by less than the critical band, varying
degrees of dissonance is heard.
The most dissonant/least consonant spacing of two tones is about 1/4 of a critical
bandwidth.
When two areas on the basilar membrane which are close to each other are stimulated
simultaneously, a interference or roughness is head and we call that roughness tonal,
or sensory disssonance. |
BACK INDEX BIBLIOGRAPHY
i END OF COURSE i
|